Skip to main content
\(\renewcommand{\chaptermark}[1]{\markboth{\MakeUppercase{ #1}}{\thechapter~ #1}} \renewcommand{\sectionmark}[1]{} \newcommand{\abs}[1]{\left|#1\right|} \renewcommand{\theenumi}{5.\arabic{enumi}} \newcommand{\norm}[1]{\left\|#1\right\|} \newcommand{\norma}[1]{\left\|#1\right\|} \newcommand{\BM}[1]{\text{\boldmath$#1$}} \newcommand{\halmaz}[1]{\left\{\,#1\,\right\}} \newcommand{\halmazvonal}[2]{\left\{\,#1\mid #2\,\right\}} \newcommand{\halmazpont}[2]{\left\{\,#1:#2\,\right\}} \newcommand{\N}{\mathbb{N}} \newcommand{\len}{\norm} \newcommand{\var}[2][]{v_{#1}\left(#2\right)} \newcommand{\vari}[2]{v_{#1}\left(#2\right)} \newcommand{\size}[2][]{s_{#1}\left(#2\right)} \newcommand{\dep}[2][]{d_{#1}\left(#2\right)} \newcommand{\sizestar}[2][]{s_{#1}^*\left(#2\right)} \newcommand{\depstar}[2][]{d_{#1}^*\left(#2\right)} \renewcommand{\headrulewidth}{0pt} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Section3.5A card trick

In this section we introduce a card trick, which is based on several mathematical ideas. In fact the trick combines several tools from this chapter. To understand how it works one should be familiar with the pigeonhole principle, proof by contradiction and some tiny amount of combinatorics. Here is the trick.

An assistant asks the audience to choose five cards from a normal deck of 52 playing cards. They can choose any five as they like. They pass those five cards to the assistant, who reveals four of them to the magician, one remains only known by the audience and the assistant. The magician looks at the four cards handed to him and announces the 5th card, the secret one.

This mathematical card trick was invented by William Fitch Cheney Jr. and it was first published by Wallace Lee in Maths Miracles in 1950. 1 William Wallace Lee, Maths Miracles, Durham, N. C. (1950)

How does this trick work? First we apply the pigeonhole principle to obtain a very important imformation. There are only 4 suits (clubs \(\clubsuit\text{,}\) diamonds \(\diamondsuit\text{,}\) hearts \(\heartsuit\) and spades \(\spadesuit\)) while there are 5 cards choosen. An application of pigeonhole principle yields that at least 2 cards must be of the same suit. The assistant and the magician have an agreement about the ordering of cards, e.g. \(A-2-3-\ldots-J-Q-K\text{.}\) There are two cards having the same suit, say \(C_1\) and \(C_2\text{.}\)

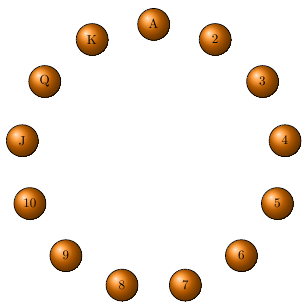
It is possible to define a distance between them. One considers the 13 same-suit cards arranged in a circle from \(A\) to \(K\) going clockwise. Given \(C_1\) and \(C_2\) one defines the distance \(d(C_1,C_2)\) as the clockwise distance from \(C_1\) to \(C_2\text{.}\) The second observation is that either \(d(C_1,C_2)\leq 6\) or \(d(C_2,C_1)\leq 6\text{.}\) This statement can be proved indirectly. Assume that \(d(C_1,C_2)>6\) and \(d(C_2,C_1)>6\text{.}\) Then there must be at least 14 cards having the same suit, a contradiction. Let us consider an example. If the two cards are \(C_1=3\) and \(C_2=J\text{,}\) then we have that \(d(3,J)=8\) and \(d(J,3)=5\text{.}\) This fact is used to decide which card is going to be at the top of the pile. Assume that \(d(C_i,C_j)\leq 6\text{.}\) The assistant will place card \(C_i\) at the top of the pile and \(C_j\) will be the hidden card. The assistant still has to decide how to order the remaining 3 cards. Here comes a tiny combinatorics involved, three cards can be ordered in \(3!=6\) different ways. That is, somehow the assistant will be able to encode the distance \(d(C_i,C_j)\leq 6\text{.}\) The 52 cards are ordered following the rules:

rule I.: \(\clubsuit\lt \diamondsuit\lt \heartsuit\lt \spadesuit\text{,}\)

rule II.: \(A\lt 2\lt 3\lt \ldots\lt J\lt Q\lt K\text{,}\)

So we have \(A\clubsuit\lt 2\clubsuit\lt \ldots\lt Q\spadesuit\lt K\spadesuit\text{.}\) Back to the last three cards. Let us denote by 1 the card having the lowest rank, by 3 the card having the highest rank and by 2 the remaining one. It is easy to make an agreement about the encoding of the distance, an example is given in the following table

\(d(C_i,C_j)\) order of the 3 cards
1 1,2,3
2 1,3,2
3 2,1,3
4 2,3,1
5 3,1,2
6 3,2,1

It is time to start the card trick! Assume that the assistant gets the following cards from the audience: \(3\clubsuit, K\clubsuit, 8\diamondsuit, 5\heartsuit\) and \(Q\spadesuit\text{.}\) Here \(3\clubsuit, K\clubsuit\) are two cards having the same suit. What about their distance? One has

\begin{align*} d(3\clubsuit, K\clubsuit)\amp = 10,\\ d(K\clubsuit, 3\clubsuit)\amp = 3\text{.} \end{align*}

The assistant has to encode 3. The ordering of the remaining three cards is \((1=8\diamondsuit)\lt (2=5\heartsuit)\lt (3=Q\spadesuit)\text{.}\) That is,

\begin{equation*} d(K\clubsuit, 3\clubsuit)=3\Rightarrow 5\heartsuit, 8\diamondsuit, Q\spadesuit\text{.} \end{equation*}

Therefore the pile of cards the assistant gives to the magician is

\begin{equation*} K\clubsuit, 5\heartsuit, 8\diamondsuit, Q\spadesuit\text{.} \end{equation*}

What card is being encoded by the following sequences of four cards?

(a) \(7\clubsuit,3\diamondsuit,J\diamondsuit,A\spadesuit\text{,}\)

(b) \(J\diamondsuit,9\clubsuit,Q\heartsuit,8\heartsuit\text{,}\)

(c) \(9\heartsuit,10\heartsuit,J\diamondsuit,6\diamondsuit\text{,}\)

(d) \(10\diamondsuit,4\spadesuit,2\spadesuit,5\diamondsuit\text{,}\)

(e) \(8\spadesuit,7\diamondsuit,7\heartsuit,3\heartsuit\text{.}\)

Which card should be the hidden card? How to order the remaining four cards to encode the hidden one?

(a) \(3\clubsuit,7\clubsuit,5\diamondsuit,2\diamondsuit,A\spadesuit\text{,}\)

(b) \(10\clubsuit,A\diamondsuit,J\diamondsuit,8\heartsuit,4\spadesuit\text{,}\)

(c) \(A\clubsuit,6\diamondsuit,K\heartsuit,7\spadesuit,8\spadesuit\text{,}\)

(d) \(7\clubsuit,8\diamondsuit,3\spadesuit,7\spadesuit,9\spadesuit\text{,}\)

(e) \(J\diamondsuit,Q\diamondsuit,7\heartsuit,10\heartsuit,3\spadesuit\text{.}\)