Skip to main content
\(\renewcommand{\chaptermark}[1]{\markboth{\MakeUppercase{ #1}}{\thechapter~ #1}} \renewcommand{\sectionmark}[1]{} \newcommand{\abs}[1]{\left|#1\right|} \renewcommand{\theenumi}{5.\arabic{enumi}} \newcommand{\norm}[1]{\left\|#1\right\|} \newcommand{\norma}[1]{\left\|#1\right\|} \newcommand{\BM}[1]{\text{\boldmath$#1$}} \newcommand{\halmaz}[1]{\left\{\,#1\,\right\}} \newcommand{\halmazvonal}[2]{\left\{\,#1\mid #2\,\right\}} \newcommand{\halmazpont}[2]{\left\{\,#1:#2\,\right\}} \newcommand{\N}{\mathbb{N}} \newcommand{\len}{\norm} \newcommand{\var}[2][]{v_{#1}\left(#2\right)} \newcommand{\vari}[2]{v_{#1}\left(#2\right)} \newcommand{\size}[2][]{s_{#1}\left(#2\right)} \newcommand{\dep}[2][]{d_{#1}\left(#2\right)} \newcommand{\sizestar}[2][]{s_{#1}^*\left(#2\right)} \newcommand{\depstar}[2][]{d_{#1}^*\left(#2\right)} \renewcommand{\headrulewidth}{0pt} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Section2.2Number of subsets

In Section 1.1 we have learned what a set is, and what its subsets are. Now, we want to count these subsets. Let us begin with some exercises.

List all subsets of \(\halmaz{1, 2, 3}\text{,}\) \(\halmaz{a, b, c}\text{,}\) \(\halmaz{\text{ Alice, Beth, Carrie } }\text{,}\) \(\halmaz{\text{ apple, banana, cherry } }\text{.}\) How many subsets do these sets have?

After solving Exercise 2.2.1, one suspects that the number of subsets depend only on the cardinality of the set, and not on the actual elements of the set. This is true in general: for example if a set has three elements, then we might as well name the elements \(a\text{,}\) \(b\) and \(c\text{,}\) and then its subsets will be exactly the same as we determined in Exercise 2.2.1.

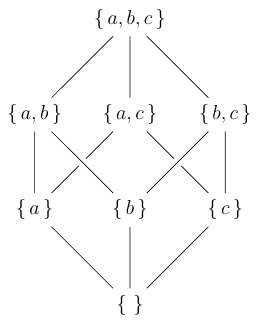
Let us try to determine the number of subsets of a set with given cardinality. Let \(S\) be a set of cardinality 0, i.e. \(S = \emptyset\text{.}\) Then \(S\) has only one subset: \(\emptyset\text{.}\) If \(S\) is a set of cardinality 1, e.g. \(S = \halmaz{a}\text{,}\) then it has two subsets: \(\halmaz{} = \emptyset\text{,}\) \(\halmaz{a} = S\text{.}\) If \(S\) is a set of cardinality 2, e.g. \(S = \halmaz{a, b}\text{,}\) then it has four subsets: \(\halmaz{} = \emptyset\text{,}\) \(\halmaz{a}\text{,}\) \(\halmaz{b}\text{,}\) \(\halmaz{a, b} = S\text{.}\) If \(S\) is a set of cardinality 3, e.g. \(S = \halmaz{a, b, c}\text{,}\) then it has eight subsets: \(\halmaz{} = \emptyset\text{,}\) \(\halmaz{a}\text{,}\) \(\halmaz{b}\text{,}\) \(\halmaz{c}\text{,}\) \(\halmaz{a, b}\text{,}\) \(\halmaz{a, c}\text{,}\) \(\halmaz{b, c}\text{,}\) \(\halmaz{a, b, c} = S\text{.}\) Figure 2.2.2 shows all subsets of \(\halmaz{a, b, c}\text{.}\) In this figure, two sets are connected if the lower one is a subset of the upper one. Table 2.2.3 summarizes our findings on the number of subsets so far.

Figure2.2.2Subsets of \(\halmaz{a, b, c}\text{.}\)
Cardinality of \(S\) Number of subsets of \(S\)
\(0\) \(1\)
\(1\) \(2\)
\(2\) \(4\)
\(3\) \(8\)
Table2.2.3Number of subsets

Guess what the rule is by looking at Table 2.2.3 and listing all subsets of \(\halmaz{a, b, c, d}\) and \(\halmaz{a, b, c, d, e}\text{,}\) if necessary.

It seems that if \(S\) has \(n\) elements, then it has \(2^n\) subsets. This is reinforced by Figure 2.2.2, where we represented the subsets of a three-element set by the eight vertices of a cube. This conjecture is true in general:

Let us denote the elements of \(S\) by \(a_1, a_2, \dots , a_n\text{,}\) that is,

\begin{equation*} S = \halmaz{a_1, a_2, \dots , a_n}\text{.} \end{equation*}

Let us try to build a subset \(T\) of \(S\text{,}\) and we count the number of possibilities to create different subsets \(T\text{.}\) First we decide whether or not \(a_1 \in T\text{,}\) that is, whether or not we put \(a_1\) into \(T\text{.}\) This gives us two choices. Now, independent of how we decided on \(a_1\text{,}\) we decide whether or not we want to put \(a_2\) into \(T\text{,}\) that is, whether or not \(a_2 \in T\text{.}\) This, again, gives us two choices. Third (independently on how we decided on the earlier elements) we decide whether or not we put \(a_3\) into \(T\text{,}\) that is, whether or not \(a_3 \in T\text{.}\) This, again, gives us two choices, etc.

This way we decide after each other for every element whether or not we want to put the element into \(T\text{.}\) On the one hand, if at some point we choose differently, then we obtain different subsets in the end. For example, if for \(a_k\) we decide differently, then in one case \(a_k\) will be an element of the subset, in the other case it will not be an element. Thus the two subsets will differ in \(a_k\text{.}\) On the other hand, all subsets can be obtained this way: for a subset \(A\) we decide to put the elements of \(A\) into \(T\text{,}\) and not put other elements in. This way, \(T=A\) will be built.

That is, by deciding for every element whether or not it should be in \(T\) we obtain all subsets exactly once. For each element we have two choices: either we put them into the subset or we do not put them into the subset. These choices on the elements are independent from each other, thus for all \(n\) elements we have

\begin{equation*} \underbrace{2 \cdot 2 \cdot \dots \cdot 2}_{n} = 2^n \end{equation*}

choices. This is the same as the number of subsets of \(S\text{.}\) Thus an \(n\) element set has \(2^n\)-many subsets.

For \(S= \halmaz{a, b, c}\) obtain all subsets using this decision algorithm.

There are different ways to obtain the same result. Another argument can be the following:

We give a draft of the proof, which can be made precise after reading about mathematical induction. Again, let us denote the elements of \(S\) by \(a_1, a_2, \dots , a_n\text{,}\) that is,

\begin{equation*} S = \halmaz{a_1, a_2, \dots , a_n}\text{.} \end{equation*}

Here, every subset either contains \(a_n\) or does not contain \(a_n\text{.}\)

First, consider those subsets, which do not contain \(a_n\text{,}\) and let \(S' = \halmaz{a_1, a_2, \dots, a_{n-1}}\text{.}\) Observe that a subset of \(S\) not containing \(a_n\) is in fact a subset of \(S'\text{.}\) Moreover, every subset of \(S'\) is a subset of \(S\) not containing \(a_n\text{.}\) That is, there is a one-to-one correspondence between the subsets of \(S\) not containing \(a_n\) and the subsets of \(S'\text{.}\)

Now, consider the subsets of \(S\) containing \(a_n\text{.}\) Observe that a subset of \(S\) containing \(a_n\) is in fact a union of a subset of \(S'\) and \(\halmaz{a_n}\text{.}\) That is, it is \(a_n\) added to a subset of \(S'\text{.}\) Moreover, if we add \(a_n\) to every subset of \(S'\) we obtain a subset of \(S\) containing \(a_n\text{.}\) That is, there is a one-to-one correspondence between the subsets of \(S\) containing \(a_n\) and the subsets of \(S'\text{.}\)

Thus, the number of subsets of \(S\) is twice as the number of subsets of \(S'\text{.}\) Continuing this argument, we obtain that the number of subsets of \(S\) is 4 times the number of subsets of \(\halmaz{a_1, \dots , a_{n-2}}\text{,}\) etc. That is, the number of subsets of \(S\) is \(2^n\) times the number of subsets of \(\halmaz{} = \emptyset\text{.}\) As the latter has only 1 subset, \(S\) has exactly \(2^n\)-many subsets.

Note, that this argument would not have been necessary, as we have already proved the statement of Theorem 2.2.5. Therefore this new proof does not make the statement any more true (in any case, a mathematical statement is either true or not true, there are no degrees to how true it is). What it provides is a different insight into how we can build subsets of a set. For example, this argument can be useful if we need certain types of subsets:

List all subsets of \(S = \halmaz{a, b, c, d}\) not containing \(d\text{,}\) and note that they are exactly the subsets of \(\halmaz{a, b, c}\text{.}\) Then list all subsets of \(S = \halmaz{a, b, c, d}\) containing \(d\text{,}\) and note that they are exactly the subsets of \(\halmaz{a, b, c}\) with \(d\) added to them.

It is an interesting coincidence that there are \(2^n\) subsets of an \(n\)-element set, and that exactly \(2^n\)-many at most \(n\)-digit binary numbers exist. Such a coincidence always makes a mathematician suspicious that there might be more to it than just accidental equality.

Encode all subsets of \(S = \halmaz{a, b, c, d}\) in the following way: for every subset \(T\) we assign an at most four digit binary number. The first digit is 0 if \(d \notin T\text{,}\) and 1 if \(d \in T\text{.}\) Similarly, the second digit is 0 if \(c \notin T\text{,}\) and 1 if \(c \in T\text{.}\) The third digit is 0 if \(b \notin T\text{,}\) and 1 if \(b \in T\text{.}\) Finally, the fourth digit is 0 if \(a \notin T\text{,}\) and 1 if \(a \in T\text{.}\) Note that this is a one-to-one correspondence between the subsets and the at most four digit binary numbers.

The idea of Exercise 2.2.8 works in general, as well:

This time it is probably more helpful to denote the elements of \(S\) by \(a_0, a_1, \dots , a_{n-1}\text{,}\) that is,

\begin{equation*} S = \halmaz{a_0, a_1, \dots , a_{n-1}}\text{.} \end{equation*}

Now, we assign an at most \(n\)-digit binary number to every subset of \(S\text{.}\) Let \(T\) be an arbitrary subset of \(S\text{,}\) and we assign a binary number to it in the following way. Its last digit (corresponding to \(2^0\)) is 0 if \(a_0 \notin T\) and 1 if \(a_0 \in T\text{.}\) Similarly, the one but last digit (corresponding to \(2^1\)) is 0 if \(a_1 \notin T\) and 1 if \(a_1 \in T\text{.}\) In general, the \((k+1)\)st digit from the back (corresponding to \(2^k\text{,}\) \(0\leq k\leq n-2\)) is 0 if \(a_k \notin T\) and 1 if \(a_k \in T\text{.}\) Finally, the first digit (corresponding to \(2^{n-1}\)) is 0 if \(a_{n-1} \notin T\) and 1 if \(a_{n-1} \in T\text{.}\) This way we assigned an at most \(n\)-digit binary number to every subset. For different subsets we assigned different binary numbers, and for every number we can easily generate the subset corresponding to it (we just need to add those elements into the subset where the digit is 1). That is, this encoding is a one-to-one correspondence between subsets of \(S\) and the at most \(n\)-digit binary numbers. By Proposition 2.1.3 we know that there are \(2^n\)-many at most \(n\)-digit binary numbers. Thus, \(S\) has \(2^n\)-many subsets, as well.

This third proof, again, gives something extra to our knowledge. Now, we have enumerated all the subsets of \(S\text{,}\) and if we are interested in the \(k\)th subset, we can easily compute it.

Let \(S = \halmaz{a_0, a_1, a_2, a_3}\text{.}\) Let us encode the subsets of \(S\) as in the third proof of Theorem 2.2.5. Compute the subsets corresponding to the binary representation of \(11\text{,}\) \(7\text{,}\) \(15\text{.}\)

Let \(S = \halmaz{a_0, a_1, a_2, a_3, a_4}\text{.}\) Let us encode the subsets of \(S\) as in the third proof of Theorem 2.2.5. Compute the subsets corresponding to the binary representation of \(11\text{,}\) \(7\text{,}\) \(15\text{,}\) \(16\text{,}\) \(31\text{.}\) Compare the results to those of Exercise 2.2.9.

Let \(S = \halmaz{a_0, a_1, a_2, a_3, a_4, a_5}\text{.}\) Let us encode the subsets of \(S\) as in the third proof of Theorem 2.2.5. Compute the subset corresponding to the binary representation of \(49\text{.}\)

Let \(S = \halmaz{a_0, a_1, a_2, a_3, a_4, a_5, a_6}\text{.}\) Let us encode the subsets of \(S\) as in the third proof of Theorem 2.2.5. Compute the subset corresponding to the binary representation of \(101\text{.}\)

Let \(S = \halmaz{a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7}\text{.}\) Let us encode the subsets of \(S\) as in the third proof of Theorem 2.2.5. Compute the subset corresponding to the binary representation of \(199\text{.}\)